Математическое ожидание. Математическим ожиданием дискретной случайной величины Х , принимающей конечное число значений х i с вероятностями р i , называется сумма:
Математическим ожиданием непрерывной случайной величины Х называется интеграл от произведения ее значений х на плотность распределения вероятностей f (x ):
 (6б
)
(6б
)
Несобственный интеграл (6б ) предполагается абсолютно сходящимся (в противном случае говорят, что математическое ожидание М (Х ) не существует). Математическое ожидание характеризует среднее значение случайной величины Х . Его размерность совпадает с размерностью случайной величины.
Свойства математического ожидания:
Дисперсия. Дисперсией случайной величины Х называется число:
Дисперсия является характеристикой рассеяния значений случайной величины Х относительно ее среднего значения М (Х ). Размерность дисперсии равна размерности случайной величины в квадрате. Исходя из определений дисперсии (8) и математического ожидания (5) для дискретной случайной величины и (6) для непрерывной случайной величины получим аналогичные выражения для дисперсии:
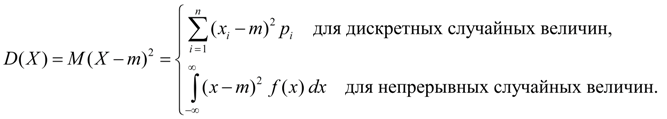 (9)
(9)
Здесь m = М (Х ).
Свойства дисперсии:
Среднее квадратичное отклонение:
![]() (11)
(11)
Так как размерность среднего квадратичного отклонения та же, что и у случайной величины, оно чаще, чем дисперсия, используется как мера рассеяния.
Моменты распределения. Понятия математического ожидания и дисперсии являются частными случаями более общего понятия для числовых характеристик случайных величин – моментов распределения . Моменты распределения случайной величины вводятся как математические ожидания некоторых простейших функций от случайной величины. Так, моментом порядка k относительно точки х 0 называется математическое ожидание М (Х – х 0 )k . Моменты относительно начала координат х = 0 называются начальными моментами и обозначаются:
![]() (12)
(12)
Начальный момент первого порядка есть центр распределения рассматриваемой случайной величины:
![]() (13)
(13)
Моменты относительно центра распределения х = m называются центральными моментами и обозначаются:
![]() (14)
(14)
Из (7) следует, что центральный момент первого порядка всегда равен нулю:
Центральные моменты не зависят от начала отсчета значений случайной величины, так как при сдвиге на постоянное значение С
ее центр распределения сдвигается на то же значение С
, а отклонение от центра не меняется: Х
– m
= (Х
– С
) – (m
– С
).
Теперь очевидно, что дисперсия
– это центральный момент второго порядка
:
Асимметрия. Центральный момент третьего порядка:
![]() (17)
(17)
служит для оценки асимметрии распределения . Если распределение симметрично относительно точки х = m , то центральный момент третьего порядка будет равен нулю (как и все центральные моменты нечетных порядков). Поэтому, если центральный момент третьего порядка отличен от нуля, то распределение не может быть симметричным. Величину асимметрии оценивают с помощью безразмерного коэффициента асимметрии :
 (18)
(18)
Знак коэффициента асимметрии (18) указывает на правостороннюю или левостороннюю асимметрию (рис. 2).

Рис. 2. Виды асимметрии распределений.
Эксцесс. Центральный момент четвертого порядка:
![]() (19)
(19)
служит для оценки так называемого эксцесса , определяющего степень крутости (островершинности) кривой распределения вблизи центра распределения по отношению к кривой нормального распределения. Так как для нормального распределения, то в качестве эксцесса принимается величина:
 (20)
(20)
На рис. 3 приведены примеры кривых распределения с различными значениями эксцесса. Для нормального распределения Е = 0. Кривые, более островершинные, чем нормальная, имеют положительный эксцесс, более плосковершинные – отрицательный.

Рис. 3. Кривые распределения с различной степенью крутости (эксцессом).
Моменты более высоких порядков в инженерных приложениях математической статистики обычно не применяются.
Мода
дискретной
случайной величины – это ее наиболее вероятное значение. Модой
непрерывной
случайной величиныназывается ее значение, при котором плотность вероятности максимальна (рис. 2). Если кривая распределения имеет один максимум, то распределение называется унимодальным
. Если кривая распределения имеет более одного максимума, то распределение называется полимодальным
. Иногда встречаются распределения, кривые которых имеют не максимум, а минимум. Такие распределения называются антимодальными
. В общем случае мода и математическое ожидание случайной величины не совпадают. В частном случае, для модального
, т.е. имеющего моду, симметричного распределения и при условии, что существует математическое ожидание, последнее совпадает с модой и центром симметрии распределения.
Медиана случайной величины Х – это ее значение Ме , для которого имеет место равенство: т.е. равновероятно, что случайная величина Х окажется меньше или больше Ме . Геометрически медиана – это абсцисса точки, в которой площадь под кривой распределения делится пополам (рис. 2). В случае симметричного модального распределения медиана, мода и математическое ожидание совпадают.
Понятие математического ожидания можно рассмотреть на примере с бросанием игрального кубика. При каждом броске фиксируются выпавшие очки. Для их выражения используются натуральные значения в диапазоне 1 – 6.
После определенного количества бросков при помощи не сложных расчетов можно найти среднее арифметическое значение выпавших очков.
Также, как и выпадение любого из значений диапазона, эта величина будет случайной.
А если увеличить количество бросков в несколько раз? При больших количествах бросков среднее арифметическое значение очков будет приближаться к конкретному числу, получившему в теории вероятностей название математического ожидания.
Итак, под математическим ожиданием понимается среднее значение случайной величины. Данный показатель может представляться и в качестве взвешенной суммы значений вероятной величины.
Это понятие имеет несколько синонимов:
- среднее значение;
- средняя величина;
- показатель центральной тенденции;
- первый момент.
Иными словами, оно является ничем иным как числом вокруг которого распределяются значения случайной величины.
В различных сферах человеческой деятельности подходы к пониманию математического ожидания будут несколько отличаться.
Оно может рассматриваться как:
- средняя выгода, полученная от принятия какого-то решения, в том случае, когда такое решение рассматривается с точки зрения теории больших чисел;
- возможная сумма выигрыша либо проигрыша (теория азартных игр), рассчитанная в среднем для каждой из ставок. На сленге они звучат как «преимущество игрока» (позитивно для игрока) либо «преимущество казино» (негативно для игрока);
- процент прибыли, полученной от выигрыша.
Матожидание не является обязательным для абсолютно всех случайных величин. Оно отсутствует для тех у которых наблюдается расхождение соответствующей суммы или интеграла.
Свойства математического ожидания
Как и любому статистическому параметру, математическому ожиданию присущи свойства:

Основные формулы для математического ожидания
Вычисление математического ожидания может выполняться как для случайных величин, характеризующихся как непрерывностью (формула А), так и дискретностью (формула Б):
- M(X)=∑i=1nxi⋅pi, где xi – значения случайной величины, pi – вероятности:
- M(X)=∫+∞−∞f(x)⋅xdx, где f(x) – заданная плотность вероятностей.
Примеры вычисления математического ожидания
Пример А.
Можно ли узнать средний рост гномов в сказке о Белоснежке. Известно, что каждый из 7 гномов имел определенный рост: 1,25; 0,98; 1,05; 0,71; 0,56; 0,95 и 0,81 м.
Алгоритм вычислений достаточно прост:
- находим сумму всех значений показателя роста (случайная величина):
1,25+0,98+1,05+0,71+0,56+0,95+ 0,81 = 6,31; - полученную сумму делим на количество гномов:
6,31:7=0,90.
Таким образом, средний рост гномов в сказке равен 90 см. Иными словами таково математическое ожидание роста гномов.
Рабочая формула — М(х)=4 0,2+6 0,3+10 0,5=6
Практическая реализация математического ожидания
К вычислению статистического показателя математического ожидания прибегают в различных сферах практической деятельности. В первую очередь речь идет о коммерческой сфере. Ведь введение Гюйгенсом этого показателя связано с определением шансов, которые могут быть благоприятными, либо напротив неблагоприятными, для какого-то события.
 Этот параметр широко применяется для оценки рисков, особенно если речь идет о финансовых вложениях.
Этот параметр широко применяется для оценки рисков, особенно если речь идет о финансовых вложениях.
Так, в предпринимательстве расчет математического ожидания выступает в качестве метода для оценивания риска при расчете цен.
Также данный показатель может использоваться при расчете эффективности проведения тех или иных мероприятий, например, по охране труда. Благодаря ему можно вычислить вероятность наступления события.
Еще одна сфера применения данного параметра – менеджмент. Также он может рассчитываться при контроле качества продукции. Например, при помощи мат. ожидания можно рассчитать возможное количество изготовления бракованных деталей.
Незаменимым мат.ожидание оказывается и при проведении статистической обработки полученных в ходе научных исследований результатов. Он позволяет рассчитать и вероятность проявления желательного либо нежелательного исхода эксперимента или исследования в зависимости от уровня достижения поставленной цели. Ведь ее достижение может ассоциироваться с выигрышем и выгодой, а ее не достижение – в качестве проигрыша либо убытка.
Использование математического ожидания на Форекс
Практическое применение данного статистического параметра возможно при проведении операций на валютном рынке. С его помощью можно осуществлять анализ успешности торговых сделок. При чем увеличение значения ожидания свидетельствует об увеличении их успешности.
Также важно помнить, что математическое ожидание не должно рассматриваться в качестве единственного статистического параметра используемого для анализа работы трейдера. Использование нескольких статистических параметров наряду со средним значением повышает точность проводимого анализа в разы.
Данный параметр хорошо зарекомендовал себя при мониторинговых наблюдениях за торговыми счетами. Благодаря ему выполняется быстрая оценка работ, осуществляемых на депозитном счете. В тех случаях, когда деятельность трейдера удачна и он избегает убытков, пользоваться исключительно расчетом математического ожидания не рекомендуется. В этих случаях не учитываются риски, что снижает эффективность анализа.
Проведенные исследования тактик трейдеров свидетельствуют о том, что:
- наиболее эффективными оказываются тактики, базирующиеся на случайном входе;
- наименее эффективны – тактики, базирующиеся на структурированных входах.
В достижении позитивных результатов не менее важны:
- тактика управления капиталом;
- стратегии выходов.
Используя такой показатель как математическое ожидание можно предположить каким будет прибыль либо убыток при вложении 1 доллара. Известно, что этот показатель, рассчитанный для всех игр, практикуемых в казино, в пользу заведения. Именно это позволяет зарабатывать деньги. В случае длинной серии игр вероятность потери денег клиентом существенно возрастает.
Игры профессиональных игроков ограничены небольшими временными промежутками, что увеличивает вероятность выигрыша и снижает риск проигрыша. Такая же закономерность наблюдается и при выполнении инвестиционных операций.
Инвестор может заработать значительную сумму при положительном ожидании и совершении большого количества сделок за небольшой временной промежуток.
Ожидание может рассматриваться как разница между произведением процента прибыли (PW) на среднюю прибыль (AW) и вероятность убытка (PL) на средний убыток (AL).
В качестве примера можно рассмотреть следующий: позиция – 12,5 тыс. долларов, портфель — 100 тыс. долларов, риск на депозит – 1%. Прибыльность сделок составляет 40% случаев при средней прибыли 20%. В случае убытка средние потери составляют 5%. Расчет математического ожидания для сделки дает значение в 625 долларов.
Основные числовые характеристики дискретных и непрерывных случайных величин: математическое ожидание, дисперсия и среднее квадратическое отклонение. Их свойства и примеры.
Закон распределения (функция распределения и ряд распределения или плотность веро-ятности) полностью описывают поведение случайной величины. Но в ряде задач доста-точно знать некоторые числовые характеристики исследуемой величины (например, ее среднее значение и возможное отклонение от него), чтобы ответить на поставленный во-прос. Рассмотрим основные числовые характеристики дискретных случайных величин.
Определение 7.1. Математическим ожиданием дискретной случайной величины называ-ется сумма произведений ее возможных значений на соответствующие им вероятности:
М (Х ) = х 1 р 1 + х 2 р 2 + … + х п р п. (7.1)
Если число возможных значений случайной величины бесконечно, то , если полученный ряд сходится абсолютно.
Замечание 1. Математическое ожидание называют иногда взвешенным средним , так как оно приближенно равно среднему арифметическому наблюдаемых значений случайной величины при большом числе опытов.
Замечание 2. Из определения математического ожидания следует, что его значение не меньше наименьшего возможного значения случайной величины и не больше наибольше-го.
Замечание 3. Математическое ожидание дискретной случайной величины есть неслучай-ная (постоянная) величина. В дальнейшем увидим, что это же справедливо и для непре-рывных случайных величин.
Пример 1. Найдем математическое ожидание случайной величины Х - числа стандартных деталей среди трех, отобранных из партии в 10 деталей, среди которых 2 бракованных. Составим ряд распределения для Х . Из условия задачи следует, что Х может принимать значения 1, 2, 3. Тогда
![]()
Пример 2. Определим математическое ожидание случайной величины Х - числа бросков монеты до первого появления герба. Эта величина может принимать бесконечное число значений (множество возможных значений есть множество натуральных чисел). Ряд ее распределения имеет вид:
| Х | … | п | … | ||
| р | 0,5 | (0,5) 2 | … | (0,5) п | … |
+ (при вычислении дважды использовалась формула суммы бесконечно убывающей геометрической прогрессии: , откуда ).
Свойства математического ожидания.
1) Математическое ожидание постоянной равно самой постоянной:
М (С ) = С. (7.2)
Доказательство. Если рассматривать С как дискретную случайную величину, принимающую только одно значение С с вероятностью р = 1, то М (С ) = С ?1 = С .
2) Постоянный множитель можно выносит за знак математического ожидания:
М (СХ ) = С М (Х ). (7.3)
Доказательство. Если случайная величина Х задана рядом распределения
Тогда М (СХ ) = Сх 1 р 1 + Сх 2 р 2 + … + Сх п р п = С ( х 1 р 1 + х 2 р 2 + … + х п р п ) = СМ (Х ).
Определение 7.2. Две случайные величины называются независимыми , если закон распределения одной из них не зависит от того, какие значения приняла другая. В противном случае случайные величины зависимы .
Определение 7.3. Назовем произведением независимых случайных величин Х и Y случайную величину XY , возможные значения которой равны произведениям всех возможных значений Х на все возможные значения Y , а соответствующие им вероят-ности равны произведениям вероятностей сомножителей.
3) Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий:
M (XY ) = M (X )M (Y ). (7.4)
Доказательство. Для упрощения вычислений ограничимся случаем, когда Х и Y принимают только по два возможных значения:
Следовательно, M (XY ) = x 1 y 1 ?p 1 g 1 + x 2 y 1 ?p 2 g 1 + x 1 y 2 ?p 1 g 2 + x 2 y 2 ?p 2 g 2 = y 1 g 1 (x 1 p 1 + x 2 p 2) + + y 2 g 2 (x 1 p 1 + x 2 p 2) = (y 1 g 1 + y 2 g 2) (x 1 p 1 + x 2 p 2) = M (X )?M (Y ).
Замечание 1. Аналогично можно доказать это свойство для большего количества возможных значений сомножителей.
Замечание 2. Свойство 3 справедливо для произведения любого числа независимых случайных величин, что доказывается методом математической индукции.
Определение 7.4. Определим сумму случайных величин Х и Y как случайную величину Х + Y , возможные значения которой равны суммам каждого возможного значения Х с каждым возможным значением Y ; вероятности таких сумм равны произведениям вероятностей слагаемых (для зависимых случайных величин - произведениям вероятности одного слагаемого на условную вероятность второго).
4) Математическое ожидание суммы двух случайных величин (зависимых или незави-симых) равно сумме математических ожиданий слагаемых:
M (X + Y ) = M (X ) + M (Y ). (7.5)
Доказательство.
Вновь рассмотрим случайные величины, заданные рядами распределения, приведен-ными при доказательстве свойства 3. Тогда возможными значениями X + Y являются х 1 + у 1 , х 1 + у 2 , х 2 + у 1 , х 2 + у 2 . Обозначим их вероятности соответственно как р 11 , р 12 , р 21 и р 22 . Найдем М (Х +Y ) = (x 1 + y 1)p 11 + (x 1 + y 2)p 12 + (x 2 + y 1)p 21 + (x 2 + y 2)p 22 =
= x 1 (p 11 + p 12) + x 2 (p 21 + p 22) + y 1 (p 11 + p 21) + y 2 (p 12 + p 22).
Докажем, что р 11 + р 22 = р 1 . Действительно, событие, состоящее в том, что X + Y примет значения х 1 + у 1 или х 1 + у 2 и вероятность которого равна р 11 + р 22 , совпадает с событием, заключающемся в том, что Х = х 1 (его вероятность - р 1). Аналогично дока-зывается, что p 21 + p 22 = р 2 , p 11 + p 21 = g 1 , p 12 + p 22 = g 2 . Значит,
M (X + Y ) = x 1 p 1 + x 2 p 2 + y 1 g 1 + y 2 g 2 = M (X ) + M (Y ).
Замечание . Из свойства 4 следует, что сумма любого числа случайных величин равна сумме математических ожиданий слагаемых.
Пример. Найти математическое ожидание суммы числа очков, выпавших при броске пяти игральных костей.
Найдем математическое ожидание числа очков, выпавших при броске одной кости:
М (Х 1) = (1 + 2 + 3 + 4 + 5 + 6)Тому же числу равно математическое ожидание числа очков, выпавших на любой кости. Следовательно, по свойству 4 М (Х )=
Дисперсия .
Для того, чтобы иметь представление о поведении случайной величины, недостаточно знать только ее математическое ожидание. Рассмотрим две случайные величины: Х и Y , заданные рядами распределения вида
| Х | |||
| р | 0,1 | 0,8 | 0,1 |
| Y | ||
| p | 0,5 | 0,5 |
Найдем М (Х ) = 49?0,1 + 50?0,8 + 51?0,1 = 50, М (Y ) = 0?0,5 + 100?0,5 = 50. Как видно, мате-матические ожидания обеих величин равны, но если для Х М (Х ) хорошо описывает пове-дение случайной величины, являясь ее наиболее вероятным возможным значением (при-чем остальные значения ненамного отличаются от 50), то значения Y существенно отсто-ят от М (Y ). Следовательно, наряду с математическим ожиданием желательно знать, на-сколько значения случайной величины отклоняются от него. Для характеристики этого показателя служит дисперсия.
Определение 7.5. Дисперсией (рассеянием) случайной величины называется математическое ожидание квадрата ее отклонения от ее математического ожидания:
D (X ) = M (X - M (X ))². (7.6)
Найдем дисперсию случайной величины Х (числа стандартных деталей среди отобранных) в примере 1 данной лекции. Вычислим значения квадрата отклонения каждого возможно-го значения от математического ожидания:
(1 - 2,4) 2 = 1,96; (2 - 2,4) 2 = 0,16; (3 - 2,4) 2 = 0,36. Следовательно,
Замечание 1. В определении дисперсии оценивается не само отклонение от среднего, а его квадрат. Это сделано для того, чтобы отклонения разных знаков не компенсировали друг друга.
Замечание 2. Из определения дисперсии следует, что эта величина принимает только неотрицательные значения.
Замечание 3. Существует более удобная для расчетов формула для вычисления дисперсии, справедливость которой доказывается в следующей теореме:
Теорема 7.1. D (X ) = M (X ²) - M ²(X ). (7.7)
Доказательство.
Используя то, что М (Х ) - постоянная величина, и свойства математического ожидания, преобразуем формулу (7.6) к виду:
D (X ) = M (X - M (X ))² = M (X ² - 2X?M (X ) + M ²(X )) = M (X ²) - 2M (X )?M (X ) + M ²(X ) =
= M (X ²) - 2M ²(X ) + M ²(X ) = M (X ²) - M ²(X ), что и требовалось доказать.
Пример. Вычислим дисперсии случайных величин Х и Y , рассмотренных в начале этого раздела. М (Х ) = (49 2 ?0,1 + 50 2 ?0,8 + 51 2 ?0,1) - 50 2 = 2500,2 - 2500 = 0,2.
М (Y ) = (0 2 ?0,5 + 100²?0,5) - 50² = 5000 - 2500 = 2500. Итак, дисперсия второй случайной величины в несколько тысяч раз больше дисперсии первой. Таким образом, даже не зная законов распределения этих величин, по известным значениям дисперсии мы можем утверждать, что Х мало отклоняется от своего математического ожидания, в то время как для Y это отклонение весьма существенно.
Свойства дисперсии.
1) Дисперсия постоянной величины С равна нулю:
D (C ) = 0. (7.8)
Доказательство. D (C ) = M ((C - M (C ))²) = M ((C - C )²) = M (0) = 0.
2) Постоянный множитель можно выносить за знак дисперсии, возведя его в квадрат:
D (CX ) = C ²D (X ). (7.9)
Доказательство. D (CX ) = M ((CX - M (CX ))²) = M ((CX - CM (X ))²) = M (C ²(X - M (X ))²) =
= C ²D (X ).
3) Дисперсия суммы двух независимых случайных величин равна сумме их дисперсий:
D (X + Y ) = D (X ) + D (Y ). (7.10)
Доказательство. D (X + Y ) = M (X ² + 2XY + Y ²) - (M (X ) + M (Y ))² = M (X ²) + 2M (X )M (Y ) +
+ M (Y ²) - M ²(X ) - 2M (X )M (Y ) - M ²(Y ) = (M (X ²) - M ²(X )) + (M (Y ²) - M ²(Y )) = D (X ) + D (Y ).
Следствие 1. Дисперсия суммы нескольких взаимно независимых случайных величин равна сумме их дисперсий.
Следствие 2. Дисперсия суммы постоянной и случайной величин равна дисперсии случайной величины.
4) Дисперсия разности двух независимых случайных величин равна сумме их дисперсий:
D (X - Y ) = D (X ) + D (Y ). (7.11)
Доказательство. D (X - Y ) = D (X ) + D (-Y ) = D (X ) + (-1)²D (Y ) = D (X ) + D (X ).
Дисперсия дает среднее значение квадрата отклонения случайной величины от среднего; для оценки самого отклонения служит величина, называемая средним квадратическим отклонением.
Определение 7.6. Средним квадратическим отклонением σ случайной величины Х называется квадратный корень из дисперсии:
Пример. В предыдущем примере средние квадратические отклонения Х и Y равны соответственно
Математическое ожидание и дисперсия - чаще всего применяемые числовые характеристики случайной величины. Они характеризуют самые важные черты распределения: его положение и степень разбросанности. Во многих задачах практики полная, исчерпывающая характеристика случайной величины - закон распределения - или вообще не может быть получена, или вообще не нужна. В этих случаях ограничиваются приблизительным описанием случайной величины с помощью числовых характеристик.
Математическое ожидание часто называют просто средним значением случайной величины. Дисперсия случайной величины - характеристика рассеивания, разбросанности случайной величины около её математического ожидания.
Математическое ожидание дискретной случайной величины
Подойдём к понятию математического ожидания, сначала исходя из механической интерпретации распределения дискретной случайной величины. Пусть единичная масса распределена между точками оси абсцисс x 1 , x 2 , ..., x n , причём каждая материальная точка имеет соответствующую ей массу из p 1 , p 2 , ..., p n . Требуется выбрать одну точку на оси абсцисс, характеризующую положение всей системы материальных точек, с учётом их масс. Естественно в качестве такой точки взять центр массы системы материальных точек. Это есть среднее взвешенное значение случайной величины X , в которое абсцисса каждой точки x i входит с "весом", равным соответствующей вероятности. Полученное таким образом среднее значение случайной величины X называется её математическим ожиданием.
Математическим ожиданием дискретной случайной величины называется сумма произведений всех возможных её значений на вероятности этих значений:

Пример 1. Организована беспроигрышная лотерея. Имеется 1000 выигрышей, из них 400 по 10 руб. 300 - по 20 руб. 200 - по 100 руб. и 100 - по 200 руб. Каков средний размер выигрыша для купившего один билет?
Решение. Средний выигрыш мы найдём, если общую сумму выигрышей, которая равна 10*400 + 20*300 + 100*200 + 200*100 = 50000 руб, разделим на 1000 (общая сумма выигрышей). Тогда получим 50000/1000 = 50 руб. Но выражение для подсчёта среднего выигрыша можно представить и в следующем виде:

С другой стороны, в данных условиях размер выигрыша является случайной величиной, которая может принимать значения 10, 20, 100 и 200 руб. с вероятностями, равными соответственно 0,4; 0,3; 0,2; 0,1. Следовательно, ожидаемый средний выигрыш равен сумме произведений размеров выигрышей на вероятности их получения.
Пример 2. Издатель решил издать новую книгу. Продавать книгу он собирается за 280 руб., из которых 200 получит он сам, 50 - книжный магазин и 30 - автор. В таблице дана информация о затратах на издание книги и вероятности продажи определённого числа экземпляров книги.
Найти ожидаемую прибыль издателя.
Решение. Случайная величина "прибыль" равна разности доходов от продажи и стоимости затрат. Например, если будет продано 500 экземпляров книги, то доходы от продажи равны 200*500=100000, а затраты на издание 225000 руб. Таким образом, издателю грозит убыток размером в 125000 руб. В следующей таблице обобщены ожидаемые значения случайной величины - прибыли:
| Число | Прибыль x i | Вероятность p i | x i p i |
| 500 | -125000 | 0,20 | -25000 |
| 1000 | -50000 | 0,40 | -20000 |
| 2000 | 100000 | 0,25 | 25000 |
| 3000 | 250000 | 0,10 | 25000 |
| 4000 | 400000 | 0,05 | 20000 |
| Всего: | 1,00 | 25000 |
Таким образом, получаем математическое ожидание прибыли издателя:
![]() .
.
Пример 3. Вероятность попадания при одном выстреле p = 0,2 . Определить расход снарядов, обеспечивающих математическое ожидание числа попаданий, равное 5.
Решение. Из всё той же формулы математического ожидания, которую мы использовали до сих пор, выражаем x - расход снарядов:
![]() .
.
Пример 4. Определить математическое ожидание случайной величины x числа попаданий при трёх выстрелах, если вероятность попадания при каждом выстреле p = 0,4 .
Подсказка: вероятность значений случайной величины найти по формуле Бернулли .
Свойства математического ожидания
Рассмотрим свойства математического ожидания.
Свойство 1. Математическое ожидание постоянной величины равно этой постоянной:
Свойство 2. Постоянный множитель можно выносить за знак математического ожидания:
![]()
Свойство 3. Математическое ожидание суммы (разности) случайных величин равно сумме (разности) их математических ожиданий:
Свойство 4. Математическое ожидание произведения случайных величин равно произведению их математических ожиданий:
Свойство 5. Если все значения случайной величины X уменьшить (увеличить) на одно и то же число С , то её математическое ожидание уменьшится (увеличится) на то же число:
![]()
Когда нельзя ограничиваться только математическим ожиданием
В большинстве случаев только математическое ожидание не может в достаточной степени характеризовать случайную величину.
Пусть случайные величины X и Y заданы следующими законами распределения:
| Значение X | Вероятность |
| -0,1 | 0,1 |
| -0,01 | 0,2 |
| 0 | 0,4 |
| 0,01 | 0,2 |
| 0,1 | 0,1 |
| Значение Y | Вероятность |
| -20 | 0,3 |
| -10 | 0,1 |
| 0 | 0,2 |
| 10 | 0,1 |
| 20 | 0,3 |
Математические ожидания этих величин одинаковы - равны нулю:


Однако характер распределения их различный. Случайная величина X может принимать только значения, мало отличающиеся от математического ожидания, а случайная величина Y может принимать значения, значительно отклоняющиеся от математического ожидания. Аналогичный пример: средняя заработная плата не даёт возможности судить об удельном весе высоко- и низкооплачиваемых рабочих. Иными словами, по математическому ожиданию нельзя судить о том, какие отклонения от него, хотя бы в среднем, возможны. Для этого нужно найти дисперсию случайной величины.
Дисперсия дискретной случайной величины
Дисперсией дискретной случайной величины X называется математическое ожидание квадрата отклонения её от математического ожидания:

Средним квадратическим отклонением случайной величины X называется арифметическое значение квадратного корня её дисперсии:
![]() .
.
Пример 5. Вычислить дисперсии и средние квадратические отклонения случайных величин X и Y , законы распределения которых приведены в таблицах выше.
Решение. Математические ожидания случайных величин X и Y , как было найдено выше, равны нулю. Согласно формуле дисперсии при Е (х )=Е (y )=0 получаем:


Тогда средние квадратические отклонения случайных величин X и Y составляют
![]() .
.
Таким образом, при одинаковых математических ожиданиях дисперсия случайной величины X очень мала, а случайной величины Y - значительная. Это следствие различия в их распределении.
Пример 6. У инвестора есть 4 альтернативных проекта инвестиций. В таблице обобщены данные об ожидаемой прибыли в этих проектах с соответствующей вероятностью.
| Проект 1 | Проект 2 | Проект 3 | Проект 4 |
| 500, P =1 | 1000, P =0,5 | 500, P =0,5 | 500, P =0,5 |
| 0, P =0,5 | 1000, P =0,25 | 10500, P =0,25 | |
| 0, P =0,25 | 9500, P =0,25 |
Найти для каждой альтернативы математическое ожидание, дисперсию и среднее квадратическое отклонение.
Решение. Покажем, как вычисляются эти величины для 3-й альтернативы:
В таблице обобщены найденные величины для всех альтернатив.
У всех альтернатив одинаковы математические ожидания. Это означает, что в долгосрочном периоде у всех - одинаковые доходы. Стандартное отклонение можно интерпретировать как единицу измерения риска - чем оно больше, тем больше риск инвестиций. Инвестор, который не желает большого риска, выберет проект 1, так как у него наименьшее стандартное отклонение (0). Если же инвестор отдаёт предпочтение риску и большим доходам в короткий период, то он выберет проект наибольшим стандартным отклонением - проект 4.
Свойства дисперсии
Приведём свойства дисперсии.
Свойство 1. Дисперсия постоянной величины равна нулю:
Свойство 2. Постоянный множитель можно выносить за знак дисперсии, возводя его при этом в квадрат:
![]() .
.
Свойство 3. Дисперсия случайной величины равна математическому ожиданию квадрата этой величины, из которого вычтен квадрат математического ожидания самой величины:
![]() ,
,
где ![]() .
.
Свойство 4. Дисперсия суммы (разности) случайных величин равна сумме (разности) их дисперсий:
Пример 7. Известно, что дискретная случайная величина X принимает лишь два значения: −3 и 7. Кроме того, известно математическое ожидание: E (X ) = 4 . Найти дисперсию дискретной случайной величины.
Решение. Обозначим через p вероятность, с которой случайная величина принимает значение x 1 = −3 . Тогда вероятностью значения x 2 = 7 будет 1 − p . Выведем уравнение для математического ожидания:
E (X ) = x 1 p + x 2 (1 − p ) = −3p + 7(1 − p ) = 4 ,
откуда получаем вероятности: p = 0,3 и 1 − p = 0,7 .
Закон распределения случайной величины:
| X | −3 | 7 |
| p | 0,3 | 0,7 |
Дисперсию данной случайной величины вычислим по формуле из свойства 3 дисперсии:
D (X ) = 2,7 + 34,3 − 16 = 21 .
Найти математическое ожидание случайной величины самостоятельно, а затем посмотреть решение
Пример 8. Дискретная случайная величина X принимает лишь два значения. Большее из значений 3 она принимает с вероятностью 0,4. Кроме того, известна дисперсия случайной величины D (X ) = 6 . Найти математическое ожидание случайной величины.
Пример 9. В урне 6 белых и 4 чёрных шара. Из урны вынимают 3 шара. Число белых шаров среди вынутых шаров является дискретной случайной величиной X . Найти математическое ожидание и дисперсию этой случайной величины.
Решение. Случайная величина X может принимать значения 0, 1, 2, 3. Соответствующие им вероятности можно вычислить по правилу умножения вероятностей . Закон распределения случайной величины:
| X | 0 | 1 | 2 | 3 |
| p | 1/30 | 3/10 | 1/2 | 1/6 |
Отсюда математическое ожидание данной случайной величины:
M (X ) = 3/10 + 1 + 1/2 = 1,8 .
Дисперсия данной случайной величины:
D (X ) = 0,3 + 2 + 1,5 − 3,24 = 0,56 .
Математическое ожидание и дисперсия непрерывной случайной величины
Для непрерывной случайной величины механическая интерпретация математического ожидания сохранит тот же смысл: центр массы для единичной массы, распределённой непрерывно на оси абсцисс с плотностью f (x ). В отличие от дискретной случайной величиной, у которой аргумент функции x i изменяется скачкообразно, у непрерывной случайной величины аргумент меняется непрерывно. Но математическое ожидание непрерывной случайной величины также связано с её средним значением.
Чтобы находить математическое ожидание и дисперсию непрерывной случайной величины, нужно находить определённые интегралы . Если дана функция плотности непрерывной случайной величины, то она непосредственно входит в подынтегральное выражение. Если дана функция распределения вероятностей, то, дифференцируя её, нужно найти функцию плотности.
Арифметическое среднее всех возможных значений непрерывной случайной величины называется её математическим ожиданием , обозначаемым или .
– количество мальчиков среди 10 новорождённых.
Совершенно понятно, что это количество заранее не известно, и в очередном десятке родившихся детей может оказаться:
Либо мальчиков – один и только один из перечисленных вариантов.
И, дабы соблюсти форму, немного физкультуры:
– дальность прыжка в длину (в некоторых единицах) .
Её не в состоянии предугадать даже мастер спорта:)
Тем не менее, ваши гипотезы?
2) Непрерывная случайная величина – принимает все числовые значения из некоторого конечного или бесконечного промежутка.
Примечание : в учебной литературе популярны аббревиатуры ДСВ и НСВ
Сначала разберём дискретную случайную величину, затем – непрерывную .
Закон распределения дискретной случайной величины
– этосоответствие
между возможными значениями этой величины и их вероятностями. Чаще всего закон записывают таблицей:
Довольно часто встречается термин ряд
распределения
, но в некоторых ситуациях он звучит двусмысленно, и поэтому я буду придерживаться «закона».
А теперь очень важный момент
: поскольку случайная величина обязательно
примет одно из значений
, то соответствующие события образуют полную группу
и сумма вероятностей их наступления равна единице:
или, если записать свёрнуто:
Так, например, закон распределения вероятностей выпавших на кубике очков имеет следующий вид:
Без комментариев.
Возможно, у вас сложилось впечатление, что дискретная случайная величина может принимать только «хорошие» целые значения. Развеем иллюзию – они могут быть любыми:
Пример 1
Некоторая игра имеет следующий закон распределения выигрыша:
…наверное, вы давно мечтали о таких задачах:) Открою секрет – я тоже. В особенности после того, как завершил работу над теорией поля .
Решение
: так как случайная величина может принять только одно из трёх значений, то соответствующие события образуют полную группу
, а значит, сумма их вероятностей равна единице:![]()
Разоблачаем «партизана»:![]()
– таким образом, вероятность выигрыша условных единиц составляет 0,4.
Контроль: , в чём и требовалось убедиться.
Ответ :
Не редкость, когда закон распределения требуется составить самостоятельно. Для этого используют классическое определение вероятности , теоремы умножения / сложения вероятностей событий и другие фишки тервера :
Пример 2
В коробке находятся 50 лотерейных билетов, среди которых 12 выигрышных, причём 2 из них выигрывают по 1000 рублей, а остальные – по 100 рублей. Составить закон распределения случайной величины – размера выигрыша, если из коробки наугад извлекается один билет.
Решение : как вы заметили, значения случайной величины принято располагать в порядке их возрастания . Поэтому мы начинаем с самого маленького выигрыша, и именно рублей.
Всего таковых билетов 50 – 12 = 38, и по классическому определению
:
– вероятность того, что наудачу извлечённый билет окажется безвыигрышным.
С остальными случаями всё просто. Вероятность выигрыша рублей составляет:
Проверка: – и это особенно приятный момент таких заданий!
Ответ
: искомый закон распределения выигрыша:![]()
Следующее задание для самостоятельного решения:
Пример 3
Вероятность того, что стрелок поразит мишень, равна . Составить закон распределения случайной величины – количества попаданий после 2 выстрелов.
…я знал, что вы по нему соскучились:) Вспоминаем теоремы умножения и сложения . Решение и ответ в конце урока.
Закон распределения полностью описывает случайную величину, однако на практике бывает полезно (а иногда и полезнее) знать лишь некоторые её числовые характеристики .
Математическое ожидание дискретной случайной величины
Говоря простым языком, это среднеожидаемое значение
при многократном повторении испытаний. Пусть случайная величина принимает значения с вероятностями ![]() соответственно. Тогда математическое ожидание данной случайной величины равно сумме произведений
всех её значений на соответствующие вероятности:
соответственно. Тогда математическое ожидание данной случайной величины равно сумме произведений
всех её значений на соответствующие вероятности:
или в свёрнутом виде:![]()
Вычислим, например, математическое ожидание случайной величины – количества выпавших на игральном кубике очков:
Теперь вспомним нашу гипотетическую игру:
Возникает вопрос: а выгодно ли вообще играть в эту игру? …у кого какие впечатления? Так ведь «навскидку» и не скажешь! Но на этот вопрос можно легко ответить, вычислив математическое ожидание, по сути – средневзвешенный по вероятностям выигрыш:
Таким образом, математическое ожидание данной игры проигрышно .
Не верь впечатлениям – верь цифрам!
Да, здесь можно выиграть 10 и даже 20-30 раз подряд, но на длинной дистанции нас ждёт неминуемое разорение. И я бы не советовал вам играть в такие игры:) Ну, может, только ради развлечения .
Из всего вышесказанного следует, что математическое ожидание – это уже НЕ СЛУЧАЙНАЯ величина.
Творческое задание для самостоятельного исследования:
Пример 4
Мистер Х играет в европейскую рулетку по следующей системе: постоянно ставит 100 рублей на «красное». Составить закон распределения случайной величины – его выигрыша. Вычислить математическое ожидание выигрыша и округлить его до копеек. Сколько в среднем проигрывает игрок с каждой поставленной сотни?
Справка : европейская рулетка содержит 18 красных, 18 чёрных и 1 зелёный сектор («зеро»). В случае выпадения «красного» игроку выплачивается удвоенная ставка, в противном случае она уходит в доход казино
Существует много других систем игры в рулетку, для которых можно составить свои таблицы вероятностей. Но это тот случай, когда нам не нужны никакие законы распределения и таблицы, ибо доподлинно установлено, что математическое ожидание игрока будет точно таким же. От системы к системе меняется лишь

